思いをめぐらすために、「スコープ」と「ステークホルダー」が決まったら、次に私たちは何をしなければならないのでしょうか。もちろん、思いをめぐらせなければならないのですが、そのために「しなければならないこと」があります。

どのような順番で、「何を、どう考えてゆかなければならないか」をできるだけ細かく決めることです。ただし、「それらの答えが、どんなものであるか」を、ひとつひとつ考えることは、早すぎます。大工さんが家を建てるとき、最初から柱を作り、柱を立てて、屋根や壁を作り出すことはできません。最初は、やはり地面をならし、柱を立てる土台を作らなければなりません。

その柱の土台を作るためには、家の形を決め、図面を描かなければなりません。図面を描くためには、どんな家を立てるのかを決めなければなりません。このどんな家を建てたいのかを決めるために、「スコープ」や「ステークホルダー」を決めることが大切だったのです。家を建てる場所や、その家で暮らす人々、何年ぐらいそこに住むのかなどを明らかにするためです。

家を建てる例で、図面を描くことから始めて、土台を作り、柱を立てて、屋根をのせて、壁を作ると言うように、家の外側を作り、さらに家の中を作ってゆくように、何をどの順番でやってゆくのかを決めることを、「手順を決める」と言います。この「手順を決める」ためには、思いをめぐらせるときに、どんな「もの」や、どんな「こと」について、思いをめぐらせるべきかについて、最初に考えることが大切です。

これは、「作業の構造を分解する」呼ばれるものです。ここで言う「作業」とは、一つ一つの細かな仕事を意味します。これは、少し大きくて、難しい仕事から考え始めて、それを行うためには、「何をしなければならないか」に思いをめぐらし、さらに、その一つ一つをもう少し細かな、もう少し簡単な仕事の組合せに分解してゆくことを言っています。この準備作業をしっかりと行うことで、良い結果がもたらされます。

私たちが何かに思いをめぐらせるとき、まず、思いをめぐらせるべき「もの」が何であるのかをはっきりさせ、それについて、これまで人々はどのように考え、どのような思いを持っていたのかを調べ、その結果に基づいて、自分は何に思いをめぐらせるべきかを決めます。これが、第一歩です。

この第一歩が終わったら、第二歩として、自分が思いをめぐらせるとき、どのような範囲まで考えに入れるべきかの「スコープ」を決め、さらにどのような人々までを思いをめぐらせるべき対象に含めなければならないかの「ステークホルダー」を決めます。そして、その準備に基づいて、第三歩として、どうやって思いをめぐらせるべきかの大きな地図を描かなければなりません。ここでの話題は、この思いをめぐらせるための地図の作り方についてです。

私たちの祖先は、古代ギリシャの時代から、簡単には分からない問題を、どのようにして明らかにし、答えを得るかについて考えてきました。その道筋(みちすじ)で、最初から難しい問題そのものを考えるのではなく、その問題の答えを得るために大切で、もっと簡単に答えが分かる問題から手を着(つ)けて、それらの簡単に分かる答えを使いながら、最初の難しい問題を解くというやり方を見つけました。古代ギリシャ時代のエジプトの数学者であったエウクレイデスは、そのような簡単に分かる定理を証明し、その証明された定理を使って、もっと難しい定理を証明する方法を使っていました。

数学者のビタゴラスから、このような数学的方法を学んだ哲学者のプラトンは、このやり方を私たちが思いをめぐらせる方法に使うことを考えていたようです。この方法を使おうとすると、私たちの身の回りに起こることで、簡単に答えが分かる問題について、全ての問題と答えを準備してから、もっと難しい問題を考えなければなりません。これは大変なことで、いくら時間があっても、なかなか仕事は進みません。そこで、逆の方法を考えるようになりました。それは、最初に簡単には答えが見つからない問題がどのようなものであるかを明らかにして、その問題を解くために必要な、少し解決が簡単な問題に思いをめぐらせる方法でした。

数学者のエウクレイデスは、平面上での幾何学を、点や直線の定義から始めました。これは、平面上のものの形について思いをめぐらせるために、絶対に欠かすことのできないものだからです。そして、平行線の公理のように、決まりごととして受け入れるべき約束ごとを決めました。その上て、正しいことを定義や公理から導ける事実を定理として示し、それが正しいことを示す「証明」を説明として付けます。このため、分かりやすい事実(定理)から始めて、少しずつ分かりにくい事実(定理)へと積み上げてゆくやり方が採られています。これは、「簡単なものから始めて、少しずつ難しいものにしてゆく」方法です。

この方法の欠点は、私たちが解きたい問題にゆきつくまでに、数多くの簡単な問題(定理)についての証明をしなければならない点です。解きたい問題に直線的に結びつくように、必要な定理(解くべき問題)を明らかにして、さらにその定理を証明するために必要になる、より細かな問題についての定理を明らかにし、証明するようにします。このようにしてゆくと、私たちが解きたいと思っている問題に直接関係する定理の証明以外に、直接関係しない定理を証明する必要はありません。ですから、思いをめぐらせる努力や、証明にかかる時間を最も少なくすることができます。つまり、最も効率の良い歩方法になります。

このように思いをめぐらせる問題について、最終的に解くべき問題を明らかに示すことから始めて、つぎに、その問題を解くために解くことが必要になっている次の問題を明らかにして、その新しい問題を解くための方針を明らかにすることが必要になります。このように、最初の問題を解くために必要になる問題を「次の水準」の問題として、その水準の問題を全て明らかにします。それが終わったら、そのようにして明らかにされた個々の問題に思いをめぐらせるのではなく、その問題を解くために必要になる、「より簡単な問題」としてどのようなものがあるのかについて、思いをめぐらせます。このようにして、一段ずつ「水準を下げてゆく」やり方です。

この方法を続けてゆくと、解決に必要な細かな問題の数は、水準を下げるに従って、どんどん増えてゆきます。しかし、一つ一つの問題は、少しずつ解決がし易くなっています。そして、水準がどんどん下がってゆくと、最後には、簡単に解くことができる、「とるに足らない問題」にまで分解されてゆきます。そのため、この「とるに足らない問題」は、すぐに解決されます。この最初の問題から、最も細かく、解決の簡単な「とるに足らない」問題までを、上の水準から始めて、最も低い水準のものまでを、ひとつひとつ言葉で書いて表にまとめてゆくと、大きな表を作ることができます。この表に示されるのが、解くべき問題を整理して示した「問題の分解表」になります。

例えば、江戸時代に、江戸の日本橋でお店を構(すま)えている商店の主が、その妻と一緒に、来年、伊勢神宮へお参りに行こうと考えたとしましょう。お供に、店で働いている小僧さんを一人連れて行くとします。この「お伊勢参りの旅の計画」に思いをめぐらせるとき、何について考えなければならないかを整理すると、下の図のようになります。この図では、上の四角で囲まれた問題を考えるためには、そこから直線で結ばれた下の四角の中に書かれている問題に答えを出さなければなりません。このようにして、「お伊勢参り」の問題を、少し深く考えてゆくと、図の中に描かれているように、3つの少し難しい問題と、6つの簡単な問題を解いてゆかなければならないことが分かります。

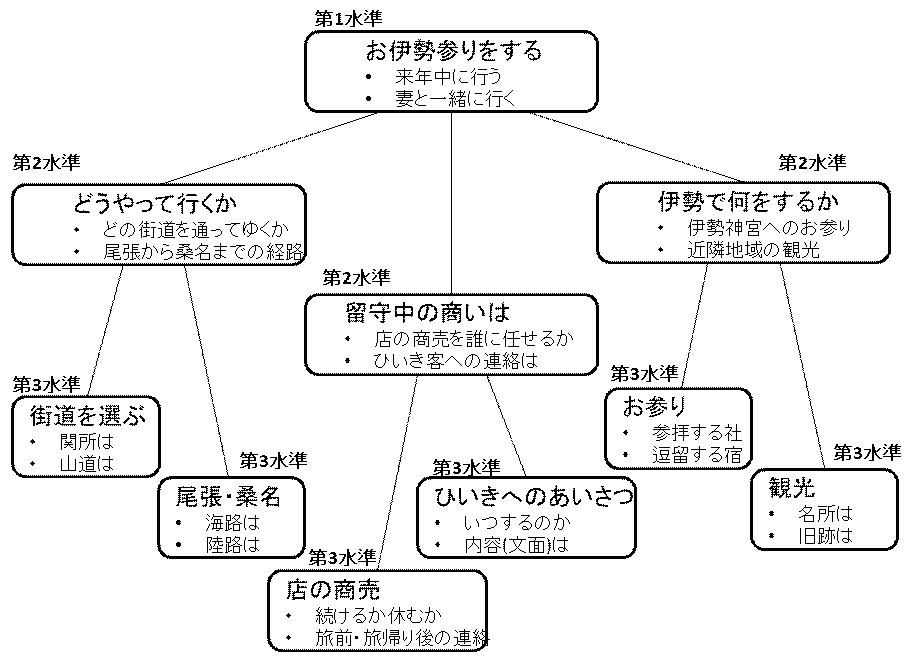
この例では、お伊勢参りに行くために、最初に東海道で行くか、中山道で行くのかなどの、どの道を通ってゆくのかを決める問題、また、名古屋から桑名まで、陸路を徒歩で行くのか、それとも船で海を渡るのかを決める問題を解くこと、2番目に、お伊勢参りの間、店の商売を、どうしてゆくのかや、大切なお客に前もって伝える方法を決める問題を解くこと、最後に、伊勢に到着してから、何をするのかの問題を解くことに思いをめぐらせなければならないことを、第2水準の問題に挙(あ)げています。さらにそれらの問題に答えを出すために、

• (第2水準)　どの道を通ってゆくのかを決める
• 江戸から名古屋までを「どの街道を選んで行くか」
• 「名古屋から桑名までの間を海路で行くか陸路で行くのか」
• (第2水準)　お伊勢参りの間、店の商売を、どうしてゆくのかや、大切なお客へ前もって伝える方法を決める
• 「一時的に店を閉めるか、続けるか」と「そのお知らせをどのように客に伝えるか」
• 「旅行の前と後のひいき先へのあいさつを、いつ、どのような形でするか」
• (第2水準)　伊勢に到着してから、何をするのかのを決める
• 「伊勢でどの神様の社にお参りをするか」
• 「周辺の夫婦岩など、どの観光地を訪れるか」

この図の第3水準の問題についての答えは、簡単に出せるので、あまり時間を書ける必要はないでしょうが、答えにいくつかの案があると思われる問題の場合、個々の案の良い点と悪い点を、よく吟味(ぎんみ)する必要があります。そのようないくつかの案の中から、最も良いと思われるものを選ぶ作業には、少し時間がかかるかも知れません。例えば、「留守中の商いをどうするか」の問題では、「店を開け、商いを誰かに任せる」の問題では、具体的に誰に「主人である自分の代わりを頼む」かを決めなければなりません。例えば、「自分の息子に任せる」や「番頭に任せる」など、いくつかの案が考えられます。それらの案の中から良い案を選ぶことは、簡単でないでしょう。例えば、「息子は若すぎる」や「番頭は歳をとり過ぎていて、激務に絶えられない」などです。問題に対する答えは、いつも良い答えがあるとは限らないからです。とは言え、考えられる限りにおいて、「最も良い」と思われる案を選ばなければなりません。

この例のように、順序だてて思いをめぐらすことによって、できるだけ考えることに「もれ」がないようにします。「もれ」があって、そのことに気づかないままにしてしまうと、そのことが実際に起きた時、大変なことになります。例えば、お伊勢参りに行っている間に、大地震が来て、店が破壊され、商売も大変なことになるかも知れません。そんな時でも、主人である自分と同じように、店や商売の立て直しができる「留守番(るすばん)」を置くことは、店の商売を続けてゆくためには、大変重要なことになります。「そんな大切なことを忘れるわけはない」と思うかもしれませんが、実際に思いをめぐらせてゆくと、一つ一つの細かな問題で頭が一杯になり、広い視野でものを考えられなくなることが、時々あります。そのような「もれ」をなくすために、このような手順で考えてゆくことが大切です。問題を細かく分解している間は、一つ一つの問題の答えを考えてはいけません。答えは、後で、一番下の問題から考えてゆきます。下の水準の問題に対する答えが見つかると、その上にある問題の答えは簡単に見つかるはずです。

現代の進んだ社会では、このように大枠を決めて、その大枠に沿(そ)って思いをめぐらすやり方が普通になっています。これによって、人間が起こしがちな失敗を防ぐように注意しているわけです。特に、解決しなければならない問題から始める、新しい方法の場合には、このような「ぬけ」や「もれ」が出ないようにする注意が大切です。この逆転(ぎゃくてん)の方法では、考えの「ぬけ」や「もれ」が、解決策全体を意味のないものにしかねないからです。後から、それに気づいたのでは遅いからです。このように「自分が思いをめぐらさなければならないこと」を書き出して、整理し、一つ一つしっかりと答えを見つけてゆくことが、しっかりとした思いに到達するための近道なのです。この新しい「逆転の方法」で、やらなければならないことを、その手順に従って、少しずつ細かく、より簡単な問題へと分解してくやり方を、最近の言葉で、「構造化した作業の分解法(構造化作業分解法)」と呼んでいます。

(つづく)