これまで私たちは、思いをめぐらすときに、どのような順番で、どのようなことについて注意を払って準備をし、どのようなやり方で問題を考え、考えついた答えの中から、どのようにして最も良いと思われる案を選んだらよいかについて、20世紀の構造主義の方法を基礎に考えてきました。しかし、どのようにして問題から答えにたどり着くかについての考え方については、後回しにして考えを進めてきました。

その第3番目の話題として、ここでは、「どう考えるのか」について、古くから知られている第3の方法について紹介します。その方法は、古代ギリシャの哲学者であるアリストテレスが考え出した方法で、「中庸(ちゅうよう)」と呼ばれているやり方です。この方法は、現代でもよく使われている代表的な方法の1つで、様々な問題についての議論の際に、最も普通の見方に基づいた問題の捉(とら)え方をして、その問題に対する最も普通の答えを導く方法です。それは、哲学者のプラトンが考え出したイデア論の方法に対抗したもので、このやり方は極端な問題の捉え方や、極端な前提に基づいた答えを避け、多くの人々にとって受け入れやすい答えを探すための方法としても知られています。

中庸を探す方法では、ある問題について、現実に起こっている具体的な例を並べて、そこから極端な見方や考え方に基づいた方法を取り除いた例を考えて示し、それらを問題の例として説明します。つぎに、その考えるべき問題の例に対する本質的な解決策を考え、それらの中で最も普通のものを選ぶやり方です。このとき、その解決に必要な考えの中に、さまざまな条件が含まれていれば、それらの条件を、別々に説明しなければなりません。これは、正しい答えかどうかが、それらの条件に合っているかどうかで、変わってしまうからです。アリストテレスは、プラトンが言ったような普遍的に、どのような場合でも「正しい」と言える答えなど、「本当はない」と信じていました。

ここで重要なことは、アリストテレスは普遍的な問題よりも、個々の問題を特徴づけている性質を明らかにして、個々の問題をできるだけ細かく説明して、誰もが分かるようにしたうえで、議論を展開すべきであるとした点です。この数多くの個別の問題を説明できる特徴を見つけ出して、皆が分かるようにした説明を、「正しい説明」と呼びます。アリストテレスは、個々の問題を考えるよりも、そのような「それぞれの問題の違いを説明する特徴」を考える方が重要であると考えました。そのように「正しく個々の問題を説明する特徴」を明らかにした上で、問題の本質と解決策を考えようとしたのです。そのような方法をとることで、個々に異なる特徴を持った現実の問題に対して、「正しい」答えを見つけることができると言いました。

私たちが、思いをめぐらすとき、絶対にしなければならないことは、これまでに述べたやり方で、どんな問題を解かなければならないかを明らかにすることです。そして、その問題を解くための答えを見つけ出すことです。私たち人類の祖先も、この問題を長い間、考え続けて来ました。古代ギリシャの哲学者、アリストテレスは、プラトンが教えていた「普遍的な問題に対して、普遍的な答えを見出す」イデア論では、本当に正しい答えにたどり着くことはできないとして、もっと現実に合った「中庸を探す」方法を考え出しました。この場合も、プラトンと同じように、ゼノンが考え出した弁証法を基にしています。弁証法では、対立する2つの意見を比べて、それぞれの弱みを並べ、それを克服するような新しい案を作り出します。アリストテレスも、2つ以上の意見を並べ、それらの中間になるような案を見つけ出すことを教えました。

アリストテレスも、ブラトンと同じように、人間が使っている言葉は、特別な場合を別にして、基本的には個別の「もの」や「こと」のある時、ある場所での様子を物語るのではなく、個々の言葉は、それらに共通する様子について説明し、それらの言葉を組合わせることで、ある時、ある場所における、ある「もの」や、ある「こと」の様子を説明できるように作られていると考えました。そのため、実際に個別の「もの」や「こと」を説明しようとすると、正確にそれを伝えることが難しいと考えました。そのようなことから、個別の問題を説明する場合、それが「何について」、どのような時に、どのような場所で、見られた様子なのかをよく見ることで、語ろうとしている問題の、時や場所、その主体が「何であるか」を細かく説明しなければならないと言いました。それは、プラトンが言った「イデア」(または言葉)を見つけ出し、そのイデアに特別な意味を付ければよいと言ったことは、現実を物語る重要な要素を捨て去ることになり、現実から離れることになると、アリストテレスは言いました。

例えば、アリストテレスから見れば、数学で言う「平行線」は、実際に存在するものではなく、数学者が考え出し、名前を付けた架空のものでしかないのです。実際には、2本の直線をどこまで延ばしても決して交わることがない、数多くの2本の直線の例だけが存在しているのです。それは、エウクレイデスが考えたような「無限遠点でも交わらない」と言う平行の様子ではないかもしれないのです。それは、地球上の同じ緯度上にある、ある場所の近くの2点で、異なる軽度上の2本の直線は、その緯度では平行であるにも関わらず、北極と南極では、交わっていることと似ています。地球のように大きな球面の一部を切り取った平面では、平行線の性質はエウクレイドスの公理に従っているようですが、それを地球規模まで拡大すると、成り立ちません。その意味で、エウクレイデスの平行線は、数学の世界でしか成り立たない、架空の話と言えます。

アリストテレスは、そのような新しい「イデア」を作り出し、新しい問題の本質に焦点を当てることで、人間の思考(考え方)が進歩してゆくと考えたことは、ブラトンの誤りだったと言いました。ですから、現実に起きた同じようなことを説明する場合に、新しいイデアを定義して、それを説明した上で、その問題を考えることによって、人間の理解が深まると考えるのは正しい方法ではないと主張しました。例えば、ソクラテスが説いた「徳」は、ギリシャ語で普通に使われていた言葉でした。その言葉をそのまま使って、ソクラテスが説いたさまざまな「徳」の例を説明すると、普通の人々は、何を説明されているのかがはっきりとは分かりません。そこでプラトンは、「徳」と言う言葉の代わりに、「徳のイデア」が何を意味しているのかを説明し、その後で、ソクラテスが説いた「徳」を、「徳のイデア」が行われた例として説明する方法を採用しました。しかし、アリストテレスは、この「徳のイデア」を使って説明したことによって、ソクラテスが説明した「徳」の例の大切な部分が失われたと考えたのでした。

このような問題を示したうえで、アリストテレスは、新しい方法として、ある場面を考えて、そこで一人一人の人が、どのように考え、どのように振る舞うかを説明したうえで、これらの例について思いをめぐらし、それらの中で、最も普通に考えられる場面で、最も普通の人が行うだろう振る舞いを探して、それを「正しい」考え、振る舞いとすべきであると教えました。この最も普通の人が、普通に考えて「行う」と考えられる振る舞いを見つけ出すやり方を、「真ん中」を見つけると言う意味で、「中庸(ちゅうよう)」と名付けました。これは、様々な考え方や振る舞いの中から、極端な例を取り除いていって、最後に残るものが、「最も普通の答え」であり、それが最も「正しい」答えになるとする考え方です。このため、アリストテレスの方法では、「正しい答え」は、議論の対象になっている問題は、いつの時代の、どこの場所で、どのような人々によって議論されたのかによって、それが「正しいかどうか」が変わるという特徴があります。これは、プラトンが、「正しい答え」は、「普遍的」で、場所や時代が変っても、その「正しさ」は変わらないとしたことと違っています。

古代ギリシャのアテネに生まれたソクラテスやプラトンは、「徳のある行い」は、時代や場所が変わっても、「徳のある行い」であるとしました。しかし、同じギリシャでもマケドニアに生まれたアリストテレスは、ある時代にある国で、「徳のある行い」と思われていた振る舞いでも、違う時代の違う国では、「徳のある行い」とは思われないかも知れないとしました。アリストテレスにとっては、どのような状況でも、「絶対的に正しい」と言える振る舞いなど、ありえなかったようです。「絶対」と「普遍的(ふへんてき)」と言う言葉は、ここでは同じ意味です。ソクラテスやプラトンが、そのような普遍的な「正しさ」を追及したのに対して、アリストテレスは、ある条件の下での「正しさ」を追求しました。ソクラテスは、ある国の法で禁じられている行いであっても、正しいと信じられることを為(な)すべきであると教えたのに対し、アリストテレスは、法に明らかな誤りがない限り、「国の法を守って、振る舞うことが正しい」と教えました。マケドニア出身のアレキサンダー大王は、アリストテレスの教えに従い、エジプトやペルシャを攻めて、占領しました。そして、その地の人々の習慣に従った法を定めました。そのことが大帝国を築くために必要であったのでしょう。

アリストテレスの考え方は、「絶対的に正しいものなどはない」と言う基本的な考え方に基づいているため、時代や国によって、何が正しいか、どのような考え方が正しいのかは変わってきます。つまり、「全てが相対的である」という考えのもとに、何が正しいのかを考えるためには、意見の中で、「極端なものを除外する」ことが、最も間違える心配のない方法になります。現代の社会で、政治においてよく使われている民主主義の多数決原理は、このようなアリストテレスの原則を踏まえたものと言えます。これは、数学者たちが、数学の定理が正しいことを証明するのとは、全く違います。数学では、絶対的な正しさがあり、それが成り立たなければ、定理は成立しません。ここに、プラトンの考え方とアリストテレスの考え方の違いがあると言えます。とは言え、私たちが生きている人間の社会には、このプラトンの「正しさ」と、アリストテレスの「正しさ」の両方があることも事実です。私たちは、どんな問題を考えているのかによって、プラトン的な方法を使うか、アリストテレス的な方法を使うのかを、選ぶ必要があります。

現代の社会における問題を議論している時、絶対に正しいと言える答えがあるかどうかが分からない時、政治家はよく「妥協(だきょう)する」と言う言葉を使います。これは、一方の見方をすると「正しい」と言えるものでも、他方の見方では「正しい」とは言えない問題があるからです。このような問題に直面したとき、両方の見方の丁度、中間に位置すると考えられる見方に立って、両方の意見を信じている人々が歩みより、その問題を解決する答えを見つけることができます。このように、2つの見方の中間を見出して、問題の答えを出すことを「妥協する」と言います。このような「妥協」は、アリストテレスが言った、「中庸」を見つける方法を、意見の対立を解消するために応用した例です。その意味でも、アリストテレスが見つけ出したやり方は、現代の社会でも広く使われている政治的な問題解決の方法の一つです。

ここで、アリストテレスの中庸を使った、政治的問題の例として、弁証法の議論で述べた「米国と日本の戦争をはじめるかどうか」の議論を考えてみましょう。最初に、「日本は、アメリカ合衆国との戦争着手を考えるべきである」と言う立場と、「日本は、アメリカ合衆国との戦争を回避するように妥協すべきである」と言う立場について、もう一度整理してみます。

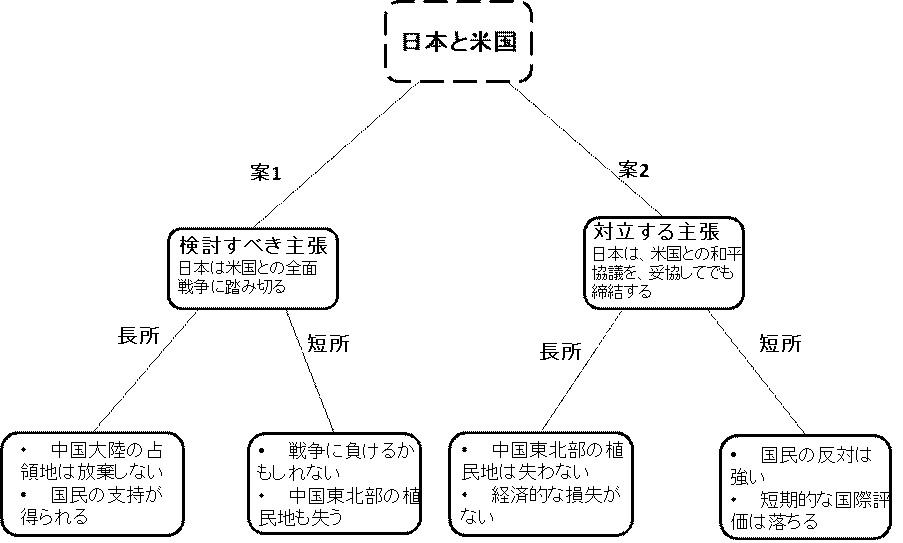
この2つの主張の良い点と悪い点を比べてみましょう。

• アメリカ合衆国との全面戦争に着手する
• 良い点
• 国民の多数からの支持を得られる
• 中国大陸での政府軍との戦いは、日本軍が優勢であり、この時点で占領地を放棄しなくて良い
• 悪い点
• 将来、アメリカ合衆国との全面戦争に負けた場合、中国大陸において、中国東北部を含めて、これまでに占領した全ての地域を失う
• アメリカ合衆国と日本との経済力を比べると、日本の経済力は劣っており、長期に渡って戦争を続けることは難しく、負けることも考えられる

• アメリカ合衆国政府と協議を続け、妥協し、合意を結ぶ
• 良い点
• アメリカ合衆国との全面戦争は避けられるので、経済的な打撃は非常に少ない
• 天皇を中心として国民が団結することで、長期的に日本の経済力を米国と同等の水準に増強し、日本のさらなる発展を成しとげられれば、米国と対等に戦争することができるようになる
• 悪い点
• 「弱腰の対応である」として、国民や軍の兵士、若手将校からの強い反発を受ける恐れが高い
• これまで、中国大陸における戦闘で、多くの犠牲を払ったが、その結果として勝ち取った中国における占領地を放棄すれば、その見返りは全く得られなくなる。世界的にも日本の評価は下落すると考えられる

この2つの考え方は、1941年頃の日本国内での議論としては、両極端の立場に立ったものと言えます。つまり、「戦争を推進する」立場と、「和平を推進する」立場です。さらに、それらは、「短期的に見た日本の国益を重視した」考えと、「長期的な視点から見た日本の発展を重視した」考え方です。当時の近衛文麿総理大臣は、この2つの極端な議論に挟まれ、天皇と日本の国家を守るためにどうするかの選択を迫られていました。

米国社会の経済力・国力をよく知っていた近衛首相は、アメリカ合衆国との全面的な戦争状態に入った場合、日本軍に勝ち目がないことを知っていました。そこで、「アメリカ合衆国と戦争をする」と言う選択を避け、そして国内世論を考えると、国民からの非難を避けられられない「アメリカ合衆国政府との安易な妥協」をせずに、日本の国民もある程度、納得させることができる「歩み寄り」を合衆国政府から引き出すように、合衆国政府との協議を進めるという方針を選びました。

これは、まさにアリストテレスが言った中庸を選んだ方針でした。平安時代から、日本の政治の中心にいて、天皇制を支えてきた藤原氏一族を代表する貴族としての態度だったと言えます。しかし、この「あいまいな」態度は、一般の日本国民にとっては、東條英機陸軍大臣の単純で明快な、「主戦論」のように受け入れられることはなく、スパイ事件も発覚したため、近衛内閣は総辞職し、東條内閣が誕生しました。そこからわずか数か月の後、日本海軍は、ハワイの米国海軍に先制攻撃をかけ、日本とアメリカ合衆国は、戦争状態に入りました。

近衛首相の考え方の要点をまとめると、以下のようになります。

• アメリカ合衆国政府と協議を続け、できるだけ合意を結ぶように努力する
• 悪い点
• 「弱腰の対応である」として、国民や軍の兵士、若手将校からの反発を受けるであろう
• 中国大陸における戦闘で、日本は多くの生命を犠牲にしたが、中国における占領地を放棄するので、短い期間で考えると、その見返りは全く得られない。しかし、長い期間で考えると、将来、日本は必ず発展するので、世界的にも日本の評価は上昇すると考えられる
• 良い点
• アメリカ合衆国との全面戦争に負けることはなく、中国大陸のほとんどの地域においては、これまでに占領した全ての地域を失うが、中国北部における日本の利権は、守ることができる
• アメリカ合衆国と日本との経済力を比べると、今の時点での日本の経済力は劣っており、長期に渡って戦争を続けることは難しいが、将来、日本の経済力がアメリカ合衆国と肩を並べる水準にまで発展すれば、対等な戦争ができるようになり、勝つこともできるようになる

この近衛首相の考えを正しく理解できる日本人は、当時、多くありませんでした。ほとんどの日本人は、アメリカ合衆国の国力や実態を知りませんでした。それだけでなく、日本軍の実情もよく知らされてはいなかったようです。日本軍の若手の将校たちも、天皇が直接、政治を行い、軍を統率すれば、日本はもっと良い国になり、強い国になると信じていたようです。そのような世論の実情と、国民の知識の水準を踏まえると、近衛首相の選択は、楽観的に過ぎていて、「正しい選択であった」とは言えなかったでしょう。このことが日本と国民を、絶望的な戦争へと向かわせました。

(つづく)