ソフトウェアとは
公開: 2021年7月20日
更新: 2021年9月7日
人類が、数や図形の問題を、個々の具体的な問題から離れて、抽象的な数や図形の問題として考え始めたのは、古代バビロニアの時代だと言われています。世界の歴史で言えば、古代メソポタミア時代、有名なハムラビ王が「ハムラビ法典」をまとめた時代です。人類は、粘土板に楔形(くさびがた)文字を使い、言葉を書き残す方法を見出したばかりの時代でした。その頃から、数学者たちは、分数を使って、我々が「無理数」と呼んでいる数を、扱う方法を考えていました。そのやり方は、近代数学で「ディアフォンタス方程式」と呼ばれるものです。
その後、古代ギリシゃのエウクレイデス(「ユークリッド」と言う名前で知られています)は、平面上に描かれる三角形や多角形などの様々な図形について考え、幾何学の基礎についてまとめました。特に、エウクレイデスは、「定義」、「公理」、「定理」、「証明」を使った数学の基本的なやり方を確立し、そのやり方は、今日の数学でも使われています。この4つの要素を組み合わせ、自分達の考えが正しいことを論理に基づいて述べることにより、人類は、誤りを含まない数学理論を構築することができるようになりました。古代ギリシゃの哲学者、プラトンは、この数学のやり方を学び、「イデア論」を打ち立てました。
ヨーロッパの世界が、古代ローマ時代から中世に移ると、数学は、東ローマ帝国を経由して、アラビア世界に伝わり、そこで発展しました。特に、数に関係した様々な問題が整理され、2次方程式の解や、3次方程式の解を求める方法などが研究されました。また、アラビア天文学の研究が進み、幾何学も進歩しました。このアラビア世界で進歩した数学は、中世ヨーロッパの十字軍によって10世紀以降のヨーロッパに伝えられ、新しく作られた「大学」の必修科目の一つとして教えられるようになりました。
ルネッサンスの時代が終わり、デカルトやライプニッツなどの哲学者による思索は、数学的なやり方を哲学にも導入し、その後の人類の思考方法を、大きく進歩させました。イギリスでは、ニュートンが、微分を発見し、現代の数学で「解析学」と呼ばれるやり方が発展し、それを物理学に応用することで、物理学が著しく発展しました。ニュートンは、観測結果と理論を橋渡しするために、観測結果から得られたデータを使って、理論が正しいことを述べるため、理論的な公式と観測データを比べるための「数値計算」の方法も考えました。これが、後の時代になって、コンピュータの利用に大きな影響を与えました。
物理学は、このニュートンの理論と観測に関する考え方によって、大きく発展するとともに、その後のイギリス社会で進んだ産業革命を進める原動力の一つとして、人類の歴史に大きな影響を与えました。19世紀から20世紀までの科学技術の大きな発展は、ニュートンの考え方を基礎にしていたと言えます。それは、数学を応用した理論の確立と、観測を基礎とした現実世界との対比による「理論と観測による正しさの確認」(「実証主義」)の考え方と言えます。
数学は、古代メソポタミア文明の古代バビロニア時代に始まったと考えられています。数(自然数)に対する理論的な理解が深まり、分数の考え方も確立されました。つまり、ある数を別の数で割った数を使って、1よりも小さな値を表す方法を発見したのです。例えば、小数点を使って我々が表現している数(有理数)の0.5は、分数を使って2分の1として表現できます。また、0.3333…のような、簡単には書くことができない数でも、分数を使って3分の1として表現できます。しかし、2の平方根、つまり我々が1.41421356…と書くような数(無理数)は、ある数を別の数で割って得られる数としては表現できません。古代バビロニアの数学者たちは、私たちが知っている、無理数を知りませんでしたた。人間は、数千年の間、無理数を知らずにいたのです。
古代バビロニアの数学者たちは、自然数の足し算、引き算だけでなく、掛け算や割り算を理解しており、その割り算の知識を使って分数を発明したのでした。このことも関係して、古代バビロニアでは、現代の我々が広く使っている「十進数」ではなく、簡単に割り算ができる「60進数」を使っていたことが分かっています。60は、12の5倍の数でもあります。12は、2、3、4、で割ることができます。さらに、60であれば5で割ることもできます。つまり、約数が多い数が60であることが、主たる理由であると考えられています。この古代バビロニア時代の60進数は、現代の社会でも角度を測り、時間を表すためにも使われています。不思議なことに、古代中国でも暦を表すために60進法が使われていました。
古代バビロニアの数学者たちは、この60進数を基礎にして、ある数の2乗や3乗などの「べき乗(じょう)」や、2乗してある数になる「平方根(へいほうこん)」についても考えていました。このような数についての理解から、私たちが今日、「方程式」と言う言葉で呼んでいる、答えが分かっていない数を「未知数(みちすう)」として、その分かっていない数を式に組み込んだ問題を解くやり方も考えていました。そのような問題の一つに、今日の数学者が「ペル方程式(ほうていしき)」と呼んでいる問題があります。それは、「ある数yを2乗した数から、別の数xを2乗した数をA倍した数を引いた結果が、1になるようなyとxを見つける」と言うものです。ここで、xやyに当てはまる数は、1、2、や3などの(自然)数でなければなりません。この問題の答えは、1つではないこともあります。
この問題で、『Aを2』としたとき、yに3を入れ、xに2を入れると、この関係を満たすことができるので、x=2かつy=3は、この方程式の1つの答えとなります。解は、もっとたくさんあります。この答えは、(自然)数を使った分数で平方根の答えを表す方法です。つまり、2分の3が2の平方根、つまり「ある数を2乗すると2になる」数に近い分数であることを示しています。Aは、求めたい平方根の数を意味しています。1.5が、1.4142135…に近い値であることを意味しています。我々が慣れ親しんでいるやり方で書き換えると、図1に示したようになります。
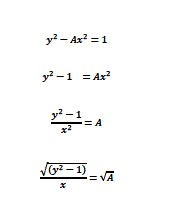
Figure 1. ペル方程式による平方根の計算
この式の展開から、yをxで割った数は、Aの平方根に近い値で、誤差は1をxで割った程度になることが分かる。例えば、2の平方根は、3を2で割った数に近い。つまり、1.5に近い値と言える。古代バビロニアの人々は、このようにして2の平方根の値を決めていたのです。
その後、古代ギリシャの数学者、エウクレイデス(英語読みはユークリッド)は、現代の数学の基礎となるやり方を確立しました。それは、数少ない用語の「定義」と、誰もが成り立つことを認める「公理」から初めて、公理に基づいて論理的に説明できる「定理」と、証明されている定理と公理から説明できる定理、そして定理が正しいことを述べる「証明」の3つの基本的な要素だけで、誤りのない定理を積み上げながら、複雑な問題を解決する方法です。エウクレイデスは、「原論」と呼ばれている書物をまとめ、現代の数学で言う「幾何学(きかがく)」の基礎を確立しました。幾何学とは、図形に関する基本的な性質を議論する一連の定理と、その基になる公理からなるものです。例えば、「点」や「直線」、「平行線」に関する定義、そして定義された図形の要素にいつも成り立つ性質に関する公理、そしてそれらの要素の間に成り立つ定理などです。平行線に関する簡単な定理としては、「平行線と交わる1本の直線とがなす2つの角の互いに対応する2つの角度は、互いに等しい。」などがあります。エウクレイデスは、このような定理が正しいことを、定義、公理だけを使って、論理的に証明しました。このエウクレイデスの「原論」は、16世紀まで、ヨーロッパの大学で、数学の教科書として学ばれてきました。
中世のヨーロッパでは、11世紀になるまで数学はほとんど進歩しませんでした。キリスト教国であった東ローマ帝国が、イスラム教国のトルコによって滅ぼされ、東ローマ帝国で活躍していた多くの数学者たちが、大量のギリシャ語の文献を持ってイタリアに逃れました。このことがきっかけとなり、イタリアの諸都市で、アラビア語で書かれていた文献が、ラテン語に翻訳され、当時、イタリアのボローニャにできた大学で教えられるようになりました。エウクレイデスの原論も、アラビア語からラテン語に翻訳され、大学で教えられるようになりました。当時の大学では、エウクレイデスの原論に基づいた、図形に関する幾何学と、数の計算に関する代数(だいすう)が教えられました。代数は、現在でも英語で「アルジェブラ」と呼ばれていますが、その名前は、アラビア語の呼び方が語源です。代数では、2次方程式の『解の公式』なども教えられていました。また、3次方程式の『解の公式』も研究されていました。これは、イスラム世界で古くから研究されていた問題のひとつでした。
17世紀のヨーロッパでは、フランスでデカルトやフェルマーなどの数学者が登場し、代数学が大きく進歩しました。特に、自然数の中で、1と自分自身でしか割り切れない、「素数(そすう)」の性質に関する研究が進みました。今日の暗号理論の基になっているフェルマーの小定理などが発見され、メルセンヌ素数なども研究されていました。フェルマーの小定理とは、与えられる自然数をaとして、aとは異なる素数をpとする時、aがpで割り切れなければ、aの(p-1)乗を、pで割った余りの数は、1になるという定理です。実際にaを2として、素数pを3と置くと、2を(p-1=2)乗した数は、2×2=4となり、4を3で割った余りは、1に等しくなる。これは、ある数が素数かどうかを調べるときに便利な性質です。ただし、この条件は、数学で厳密に言う「必要条件」であり、この関係が成り立ったからと言って、その数が素数とは、必ずしも言えません。『この条件が成り立たない数は、素数ではない。』ことを言うものです。
また、メルセンヌ素数とは、「2の自然数乗から1を引いた数が素数である」と言う説ですが、特に「2の素数乗から1引いた数のほとんどは素数」であることが調べられています。しかし、「メルセンヌ数が素数である」という性質は常に成り立つものではないことが分かっています。例えば、2の10乗は1024で、1を引くと1023となり、31と33で割り切れます。このように、メルセンヌ数と呼ばれる数が、本当に素数である場合も多いのですが、そうでない場合も少なくないことが分かっています。このメルセンヌ素数は、カトリック教会の神父であったメルセンヌ神父が発見し、17世紀の数学者達に確認を求めた説であると言われています。今日でも、大きなメルセンヌ素数を見つけ出す問題は、世界中の数学者達が挑戦して続けている問題です。特にこの問題を解くためには、新しい素数を見つけることと、その新しく見つけた素数を使ってメルセンヌ素数の候補を求め、その数が素数であることを確認するための計算を高速に実行することが問題になっています。難しい問題です。
17世紀に生まれ、18世紀に活躍した物理学者のニュートンは、宇宙の天体の動きを説明するために、新しい数学の方法を生み出しました。それは、現在、「微分方程式」として知られているものです。人間に見ることができる天体や物体の運動は、ある1時点と、その前後における天体や物体の運動で、その運動の全体像ではありません。運動の始まりから終わりまでの動きを知ろうとすると、その一瞬と、その前後の動きから、動きの全体像を見出さなければならないのです。例えば、ある物体が地球上で飛ぶ運動を考えると、ある瞬間にその物体が受けている力を全て整理することができます。つまり、物体の現在の位置をxとyの座標で表し、上下方向の動きの変化をyの変化量として表し、進行方向への動きの変化をxの変化量として、それらの変化量をdy、dxとします。物体が時刻tにある進行方向上の位置をx、その地面からの高さをyとすると、x方向の変化は、物体が発射された時間(t=0)での発射の速度、すなわち、物体が発射されたときの進行方向への速度に比例した分だけ進みます。さらに、y方向の変化は、物体が発射されたときの垂直方向への速度に比例した分と、地球の重力によって物体が落ちる速度に従う分で決まる変化分だけ変わります。物体が落ちる速度は、重力加速度(約9.8m/秒の2乗)に従います。従って、時刻tにおける物体の垂直方向の位置の変化は、
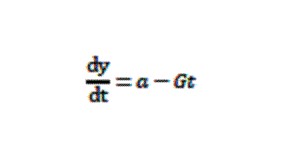
Figure 2. 微分方程式による弾丸の位置の計算
で与えられます。Gは、地球上で1秒間にものが落ちる時に重力で加速する速さを示す値(9.8)です。aは、大砲が弾丸を発射したときの弾丸の速さです。例えば、大砲によって打ち出された砲丸が描く軌道の高さは、この微分方程式で表されます。時刻ゼロでのyの値はゼロ(地上の高さ)であり、次にyがゼロに等しくなる時の時刻が、弾丸が地上に落下する時刻です。これが、ニュートンが見出した物体の動きを表す「運動方程式(うんどうほうていしき)」です。
ニュートンは、この運動方程式を解くための数学も考えました。その結果、現代の数学で言う、「微分方程式(びぶんほうていしき)」の解き方を考え出しました。この微分方程式は、微分(びぶん)の反対である積分(せきぶん)を考えることで簡単に解けます。この微分方程式を積分すると、その解は、
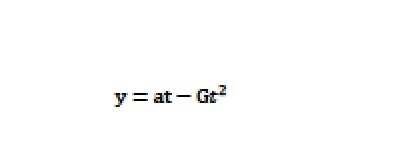
Figure 3. 微分方程式を解く
で与えられます。このyがゼロになる時刻tが、砲丸が地面に落下する時刻です。その時刻をTとする。弾丸の進行方向への距離xは、
Figure 4. 砲弾の飛行距離の計算
より、
Figure 5. 砲弾の飛行距離を表す式
で与えられます。bは、大砲が砲丸を発射したときの砲丸が進行方向へ進む速さを表す定数です。この定数は、大砲で使われる火薬の質と量によって決まります。
これより。時刻Tの時点で砲丸が到達する距離は、
Figure 6. 時刻Tまでに砲弾がとどく距離
で与えられます。
この微分方程式は、観察対象の変化を数式で表現することができれば、観察対象がどのような動きをするのかを知ることができることを示しています。ニュートンが微分方程式を見出し、数学者達が、微分方程式を解く方法を研究したため、物体の動きに関する知識は、18世紀から20世紀にかけて、著しく進歩しました。このため、物理学も進歩しました。
ある物体の時刻tにおける位置()を変数xで表すと、xは時間tを独立な変数とする関数となります。その物体の位置が時間によって全く変化しないとすれば、時間が少し進んだ場合の位置の変化はないため、それを表す微分方程式は、
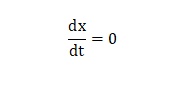
Figure 7. 微分方程式による物体の位置の計算
となります。また、その物体の位置が常に時間とともに一定の変化をすると仮定した場合、時間が少し進んだ場合の位置の変化は一定であるため、それを表す微分方程式は、
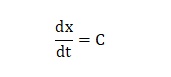
Figure 8. 微分方程式による物体の位置を表す式
となります。Cは、物体の位置がわずかの時間で変化する量を現わす定数です。この微分方程式を解くと、時刻tにおける物体の位置xは、
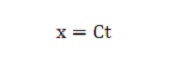
Figure 9. 物体の位置を表す式/b>
で与えられます。これは、物体の位置が時間とともに一定の変化を続けるからです。さらに、その物体の位置が時刻tにおけるxの位置に比例した分だけ変化すると仮定すると、時間が少し進んだ場合の位置の変化が現在のxの位置に比例するため、それを表す微分方程式は、
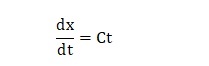
Figure 10. 時刻tにおける物体の位置
となります。この微分方程式を解くと、時刻tにおける物体の位置xは、
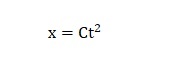
Figure 11. 時刻tにおける物体の位置
で与えられます。定数Cは、物体の位置の変化が、その物体の現在の位置に比例した分だけ変化する時の比例定数に相当します。時刻tから少し時間が進むときに、xの位置がその時刻にある位置に比例する分だけ変化をするので、全体として最初からの動きを考えると、xの2乗に比例した分だけ変わってゆくこととなります。
大砲を撃った時に大砲から発射された弾丸が発射後t時間後に到達します、大砲からの距離は、砲弾の地上からの高さがゼロになる時刻Tまでに進む距離に等しく、その距離は、大砲が砲弾を打ち出したときの砲弾の速度Aに時刻Tをかけた値に等しくなります。さらに、その時刻Tを求めるためには、砲弾を打ち出したときに、砲弾が空に向かって進む速度をBとし、砲弾が受ける地球の引力から受ける砲弾を地表へ向かわせる力が互いに影響しあった結果として、砲弾の地表からの飛行高度をyで示すと、
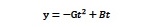
Figure 12. 時刻tにおける物体の高度
で与えられます。ここで、Gは重力加速度で、9.8メートルに等しい値です。Bは、大砲の砲身が地表との間でなす「仰角」によって決まり、仰角が45度の場合、大砲の射出速度の約3分の2になります。この式を使って、yがゼロとなる時刻を求めると、時刻Tが求まります。つまり、
となり、大砲がある場所から着弾点までの距離は、
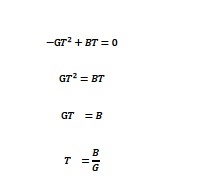
Figure 13. 着弾点までの距離を与える式
で与えられます。この例で示した大砲の仰角が45度の時、砲弾は最も遠くまで到達します。それは、それが大砲の砲弾を最も高い高度に到達させ、そのことが砲弾の滞空時間を最も長くし、結果として最も遠くまで飛ばすことになるからです。
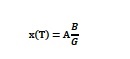
Figure 14. 着弾点までの距離を与える式
このように、18世紀までの数学は、人類が自然現象に対する理解を深めることに大きく役立ちました。しかし、それまでの数学は、人類が「ものごと」を考えるための方法を良くするための指針を与えるものではありませんでした。それが変化し始めたのは、19世紀になって、イギリス社会で産業革命の結果がはっきりし始めた頃からです。